Even unobfuscated code is difficult to understand. Look at this function. Can you tell its purpose?
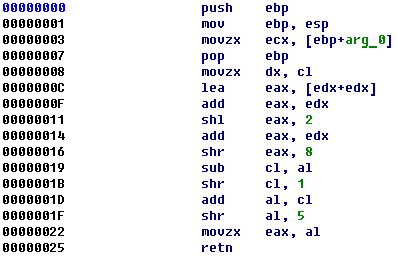
The answer is very simple. Here it is:
unsigned char div61(unsigned char x) { return x / 61; }
In is just a division by 61!
At the first sight it looks overly complicated. Why not use the div instruction? The reason is that this longer(!) code is faster.
Then, when we understand this, the code still looks like a magic. There is nothing like division there, only all kinds of shuffling bits to the left and to the right. If you are really curious how this code works, consider reading this article by Torbjorn Granlund and Peter L. Montgomery:
Division by Invariant Integers using Multiplication
It would be nice to have code sequences like this automatically deciphered. Once we know the answer, the mystery disappears and only the tedious work of finding the dividend remains. A decent program analysis tool or decompiler definitely could (and should) do it.

