In May a contest was open on Datarescue’s forum:
http://www.datarescue.com/ubb/ultimatebb.php?/topic/4/375.html
There were some nice tries but nobody guessed it right.
It seems Datarescue will have to repeat the contest with another question 🙂
If you are curious to learn the correct answer, please read on.
For IDA Pro a program consists of functions.
A function has many attributes, like the entry point and frame size.
It may also have some locally defined items: labels and stack based variables.
Usually IDA automatically handles the stack variables: it creates stack variable
definitions (stkvars)
and converts the referencing operands into the stkvar type. Let’s consider
this source code:

The first sample function has been analyzed perfectly well:
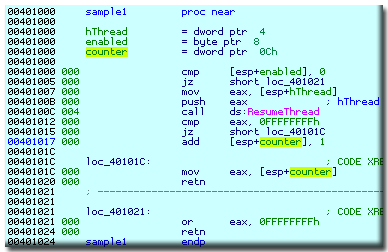
There are three stack variables. They were created by IDA because of very recognizable
stack references in the ESP+n form.
I gave the stack variables meaningful names:
hThread, enabled, and counter.
In the green column after the addresses, IDA displays the stack pointer values.
The displayed values represent the difference between the initial value of the stack
pointer at the function entry point and the current value.
Look at the push instruction in this code. Right after it the difference
becomes 4.
There is no corresponding pop instruction, but this is not a mystery
for knowledgeable programmers working with MS Windows API:
functions with so called stdcall
1
calling convention remove their arguments from the stack.
Fortunately, IDA knows about such functions
and carefully adjusts the stack after the call. The stack pointer
at 401012 becomes 0 as it should. Just as a sidenote, the information
about the stdcall functions
comes from the IDS files in the ids subdirectory and you can handle them with
special utilities available on Datarescue’s site.
But what happens when IDA does not know about the calling convention?
Look at this wrong listing:
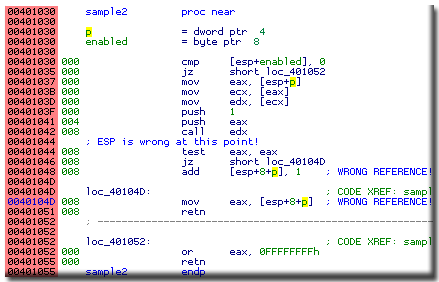
At 401042 there is an indirect call and there are 2 push instructions just before it.
By examining the whole function we can tell with 100% certainty that the called function
must remove its arguments from the stack. Otherwise the return instruction at 401051
could not return to the caller because the stack would still contain the additional bytes.
IDA did not know what to do with the call and left it as is.
As a consequence, the stack pointer values after the call became incorrect and
all references using ESP were incorrect too.
For example, the instruction at 401048 does not increment p but the third operand.
This was completely missed by IDA.
The current version of IDA behaves like this: it has a very simple stack tracer
which does not analyze the whole function but just traces
individual sp modifications for each instruction. Naturally, it fails
as soon as any indirect call or a call to a function with unknown effect
on the stack is made. To tell the whole truth, there is a mechanism to handle
the simplest cases when the function ends after several pushes and a call.
But this mechanism is too simple and fails more than succeeds.
The stdcall function problem is important for MS Windows programs. This calling
convention is a de facto standard for MS Windows API. It is also used in many projects
since it is the only calling convention which guarantees compatibility between different
programming languages. For example, all IDA exported functions are stdcall (there are
some exceptions, most notably functions with the variable number of arguments; for the
obvious reasons they can not be stdcall).
The good news are that the next version of IDA will handle the stack trace much better.
The second sample function will look like this:

IDA did determine that the call removes 8 bytes from the stack, adjusted the stack pointer
and correctly represented the subsequent stack variable. The function takes three arguments,
which is correct.
This information will be propagated in the disassembly and the whole disassembly
will be better.
How did IDA determine the stdcall functions? Here is the outline of the algorithm.
First we break the function down into basic blocks
2:
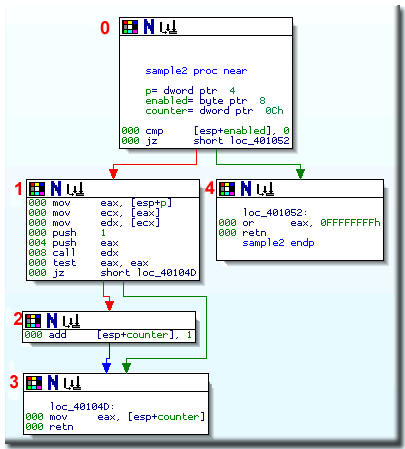
(the red numbers denote the block numbers)
The second step is to build a system of linear equations based on the graph edges
and available push/call information. For each basic block we introduce two variables: the
value of the stack pointer at the entry and at the exit of the block.
For our sample function, the following equations have been generated:

The equation for block #1 uses inequality since the block may leave the 8 bytes on stack
as well as may clean them.
The third (last) step is to solve the equations and apply the results to the disassembly.
My first urge was: “hey, this is so simple, I’ll just solve these equations”.
So I implemented a tiny Gaussian elimination method (there were no inequalities in the equations yet)
and was happy with the result until a test.
The real wild world of programs turned out to be much more versatile and
weird, if not hostile. There were all kinds of functions.
Some functions did change the stack pointer so at the function exit it was different from its initial value.
I found their names and excluded them from the analysis.
Some functions were malformed.
There was no point of trying to analyze them.
Some functions gave so little information
about the stack pointer that it was not enough to build a sufficient number of equations.
The equations would have too many (infinite) number of solutions. I needed only one.
To choose only one solution among many possible, I had to restate the stack tracing
as an optimization problem and solve it with the simplex method 3.
The optimization criteria was to find the minimum of the sum of all variables.
This is not completely correct but gives nice results in practice.
Probably it works well because compilers try to consume as little stack as
possible and do not issue meaningless push instructions 4..
I also had to set the low bounds for all inner variables. Inner variables are
all variables which are not in0 and outn where n is the number of a basic block
ending with return. Without the low bounds the solution is incorrect and can not
be applied.
The last step was to apply the obtained result back to the disassembly, which was straightforward.
There were some nasty questions, the biggest one was how to resolve
the situation with several indirect calls in a basic block.
A simple heuristic of assigning as much push instructions to a call a possible worked well enough.
The next version of IDA will use an external DLL to solve systems of linear equations.
It’s name is COIN/Clp and it comes from IBM.
This library is an overkill because our equations are derived from a graph and can be
solved in a simpler way but I opted for it because it was not obvious that something simple
would fit. In fact, it was the contrary: I constantly had to switch from simple
approaches to more sophisticated ones until the result was acceptable.
Alas, the new method does not handle all cases. There will still be stack analysis failures,
especially when the function uses structured exception handlers (SEH). Overall,
the success rate is about 97%.
I’d compare having a correct stack pointer trace to having a very flat and solid
workbench. It is not a big deal if you have a nice one. You do not even notice it when
everything works correctly. Things are different when your table is shaky and
your efforts are spent to keep it stable (look again at the wrong listing).
1. More about calling conventions:
http://blogs.msdn.com/oldnewthing/archive/2004/01/08/48616.aspx
2. Basic blocks are used quite often for program analysis:
http://en.wikipedia.org/wiki/Basic_block
3. More about simplex method:
http://en.wikipedia.org/wiki/Simplex_algorithm
4. I have to admit that I encountered some compiler-generated functions which were allocating stack space
before each call and releasing immediately after it. The allocated space was not used at all.

